Written by Bob Mecham.
To take the AccuDraw with Popup Calculator one step further I will show some of the uses of “=” function. The popup calculator allows you to do complex expressions. You can include more than one operator and have the use of parentheses. For example when using AccuDraw to construct a 20” diameter pipe in a profile with a vertical exaggeration of 4, the expression would be “=20/12)*4” this would give me the correct height of the pipe.
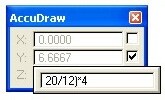
Notice there is not a matching parenthesis at the beginning however it did come up with the right solution. Also be aware that as the calculation is being typed it is being shown graphically on your screen.
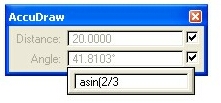
There is also the use of trigonometric values with popup calculator sin, cos, tan, asin, acos, and atan, are all available. In this example we will find the Arcsine value.
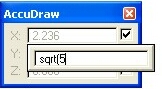
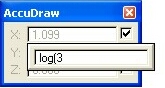
Two other functions that I am aware of are “sqrt” which will calculate the square root of the number and “log” which will calculate the natural log of the number.
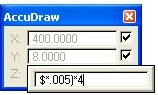
Unique to AccuDraw is the dollar sign “$”which will allow the user to utilize a distance or value that was typed in AccuDraw. The “$” will work when used in conjunction with popup calculators core math functions +, -, *, /, however “$” will not work with any of the scientific functions.

Curious behaior of PI in an expression
Try the following expression to draw a circle to a specific area, say 10,000 mm2
Select Place Circle command and place a data point then select the “=” function and key in the following expression
sqrt(10000/pi
it does not work. What does work is the following expression
sqrt(10000/3.14159265
pi seems to work in all other equations but not this one and I have tried different ways of using pi ie PI ‘pi’ ‘PI’ (pi) (PI)
Hi Mike that is interesting. I never came across that before. The only way I could do it was by separating the formula and doing 10000/pi then taking the sqrt which is not efficient at all. I will look into it a little further and see what I can find out.